Informatique Scientifique en C++

Cours

mardi 15/02/2011 (ID) : Les classes pour la méthode des éléments finis 

• Modélisation du plan R2.
  
• Triangulation d'un domaine 2D et fichier (msh) contenant un maillage.
  
• Les classes pour les éléments finis (R2, Label, Vertex, Triangle, Mesh) (voir polycopié, paragraphe 4.8)

 

  

vendredi 18/02/2011 (FH)

• Méthode des éléments finis 2D : coordonnées barycentriques, formules de quadrature, construction de la matrice du système (voir polycopié, paragraphes 4.4-4.7)
  
  

TD

Mardi 15 février : soutenance du projet 1 pendant la séance de TD

 

 

---

Les exercices de la semaine 6 à regarder absolument ! 

Exercice 01 : les classes RNM optimisée pour la modélisation des tableaux à 1,2, ou 3 indices

1. Télécharger tous les programmes du dossier  semaine_06.

    

2. Compiler et exécuter le programme ExUtilisationRNM.cpp  Analyser la syntaxe pour l'utilisation des classes RNM !
   

    

Exercice 02 : utilisation de la méthode du gradient conjugué avec une matrice virtuelle

1. Télécharger tous les programmes du dossier  semaine_06.  La méthode du gradient conjugué est programée dans GC.hpp.
   Pour une description théorique de la méthode voir ce document pdf
   

    

2. Compiler et exécuter le programme Ex_test_GC.cpp  Analyser les deux méthodes utilisée pour résoudre le problème du Laplacien 1D  !
   -u''(x) = 1, pour 0 < x < 1, avec les conditions aux limites u(x=0)=0, u(x=1)=0
   solution exacte : u(x)=x(1-x)/2;

                                  

                                  

---

Exercice 1 : la modélisation du plan R^2 : la classe R2

1. Télécharger les programmes   R2.hpp  et test_R2.cpp.

    

2. Compiler et exécuter le programme  test_R2.cpp. Analyser la syntaxe pour l'utilisation de la classe R2!

Exercice 2 : utilisation de FreeFem++ pour générer un maillage de type éléments finis triangulaires 

1. Pour télécharger et installer le logiciel FreeFem++, voir www.freefem.org
   
2. Téléchargez et exécuter  les programmes (scripts) FreeFem++  cercle.edp et cercle_12.edp
   
3. Analyser le fichier cercle.msh généré ; il contient le maillage et sera utilisé dans vos applications C++.
   
4. Ecrire un script  .edp  pour générer le maillage d'un rectangle [-A,A]*[-B,B] ; attention, la définition paramétrique de chaque frontière doit respecter le sens de parcours trigonométrique.

Exercice 3 : utilisation des classes pour les éléments finis

1. Télécharger l'archive   semaine_07.tar.gz  

2. Désarchiver dans votre dossier local (tar zxvf  semaine_07.tar.gz)
   
3. Compiler et exécuter le programme test_Mesh.cpp
   
                          g++ test_Mesh.cpp Mesh2d.cpp -I./RNM-v3 -o test
                     ./test cercle.msh
Attention, le fichier cercle.msh doit exister (voir l'exercice précédent).


4. La solution est écrite dans le fichier plot ; pour la visualisation, utiliser sous Gnuplot                         


                     splot "plot" using 1:2:3 w l
                     splot "plot" using 1:2:4 w l

---

Exercice  4 : solution d'un laplacien sur un carré

 

1. Téléchargez l'archive semaine_07.tar.gz
    
2. Désarchiver dans votre dossier local (tar  zxvf  semaine_07.tar.gz)
   

3. Générer le maillage d'un carré en utilisant  FreeFem++ avec le script carre.edp.

4. Compiler et exécuter le programme EF2d-2011.cpp 

   g++ EF2d-2011.cpp Mesh2d.cpp -I./RNM-v3 -o lap2d

   ./lap2d carre.msh

    

5.  la solution est écrite dans le fichier plot ; pour la visualisation, utiliser sous Gnuplot

   splot "plot" w l

    

6. Quelques explications :: ce programme résout par éléments finis l'EDP 2D
   
   • le domaine de calcul est un carré : le maillage est contenu dans le fichier carre.msh
   • les fonctions f et g sont données (f= -6, g= x^2 + 2 y^2 dans ce cas)
   • on va noter les matrices qui interviennent dans la méthode des éléments finis par
     
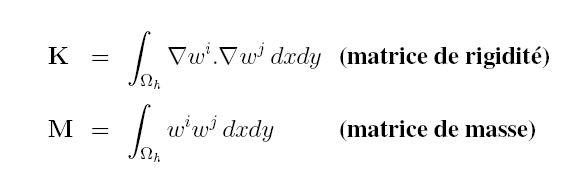
   • le système linéaire final s'écrit (la fonction f est considérée P1 pour calculer le second membre)

     K*U=M*F

   • le système linéaire est résolu par  la méthode du gradient conjugué
     

     Il faut retenir que pour la résolution d'un système AX=F, la méthode du gradient conjugué utilise que des produits A*vecteur.
     D'où l'idée de définir seulement la fonction qui calcule ce produit matrice*vecteur, sans avoir à stocker la matrice A du système.
      

   • plusieurs versions du programme seront proposées par la suite