Informatique Scientifique en C++

Cours

mardi 15/03/2011 (ID) : Introduction à JAVA  

• Caractéristiques du langage. Différences avec le langage C++.
  
• Utilisation pratique  : programmes et applets.  Syntaxe du langage.
  
• Les programmes du cours
  • hello_2011.java
    • Compilation : javac hello_2011.java
    • Interprétation et exécution : java hello_2011
  • App_hello_2011_v1.java
    • Compilation : javac App_hello_2011_v1.java
    • Ouvrir dans un navigateur web : App_hello_2011_v1.htm
  • Meme chose pour : App_hello_2011_v2.java
  
  
• Notes de cours : le chap9 du livre Simulation numérique en C++, Dunod, 2003.
  

 

  

vendredi 18/03/2011 (FH) : Optimisation des programmes pour résoudre le problème du laplacien

• Utilisation des maps pour construire la matrice creuse du système linéaire
• Génération d'une structure de matrice creuse simple au format COO (3 tableaux I,J,A) : voir paragraphes 5.4 et 5.8.2 de Notes de cours
  
• Les programmes du cours sont dans l'archive EF2D-2011.tgz
  

TD ::

  Enoncé du Projet 2, avec les questions de la deuxième partie (différenciation automatique, OpenGL, Java)

1. Question Q3 (différences finies) : une approximation de la dérivée par rapport à alpha au point (alpha=10) est (différences centrées): 
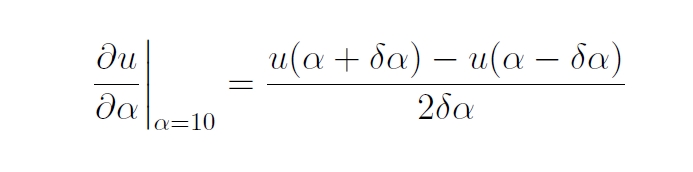
   • Cette méthode implique deux calculs (correspondant à la question Q2, point d) pour trouver
   •  
   •  Il faut tester plusieurs valeurs de  dalpha.
   • Attention, la dérivée est une fonction de (x,y) ; on peut donc faire les mêmes graphs que pour u. On vous demande d'extraire la valeur de (du/dalpha) au point de coordonnées P(0 , 0.9*L) -- comme ce point n'est pas forcement un sommet du maillage, il faut utiliser les coordonnées barycentriques pour calculer la valeur demandée (interpolation P1).

2. Question Q3 (différenciation automatique)  :  pour calculer (du/dalpha)  par diff automatique

   • téléchargez     ddouble.hpp ddouble-GC.hpp  (ou à partir du dossier  ID/semaine_10)
     utilisez dans le programme principal
     

     
     #include "Mesh2d.hpp"
     #include "ddouble.hpp"
     
     #include "RNM.hpp"
     #include "ddouble-GC.hpp"
      

    

   • toujours   dans le programme principal, les typedef à utiliser sont
     
     typedef double R;
     typedef ddouble Rdb;
      
   •  pour les variables liées au maillage, rien ne change (on ne dérive pas par rapport au maillage)

    

   • pour les variables utilisées dans le calcul de la solution (matrices, second membre, etc)
     double  devient  ddouble
      
   • initialiser le paramètre   ddouble  alpha(10., 1.);  pour obtenir à la fin de l'exécution la dérivée par rapport à alpha.

    

   • comparer avec la valeur trouvée par différences finies, toujours au point de coordonnées (0, 0.9*L) .

   
   

3. Question Q4 : visualisation avec OpenGL/Glut : Utilisez les indications suivantes pour voir comment réaliser une visualisation avec OpenGL.  Réalisez ensuite une visualisation de l'évolution en temps de la solution numérique.

   
   

   • téléchargez le programme glplotiso.cpp dans le même dossier ou se trouvent les programmes pour les éléments finis (EF2d-2011.cpp, les classes RNM, etc) ;

    

   • téléchargez le programme Makefile_glplot

    

   • compilez par la commande : make -f Makefile_glplot
     Attention : il faut éditer le fichier Makefile_glplot pour s'assuer ques les options de compilations sont compatibles avec votre système (par défaut, on utilise Linux)

    

   •   exécuter le programme par : ./glplotiso carre.msh u.sol 10.
     Attention, le programme à besoin de trois arguments :
     • le fichier maillage (carre.msh) 
     • le fichier contenant la solution u.sol (il est écrit à partir de votre programme C++ de manière habituelle
       (ofstream fic("u.sol"); fic <
     • un facteur d'amplification (valeur de type double) -- explorez son influence sur la visualisation obtenue.